LeetCode-排列组合
排列组合问题
子集、组合、排列问题就是从序列中以给定规则取若干元素构成集合的集合。本质上就是穷举所有解,而这些解呈现树形结构,因此合理使用回溯算法框架就可以一网打尽。
主要记住下面两棵回溯树,所有问题都是这两棵树的变种,关键在于剪枝的判断。
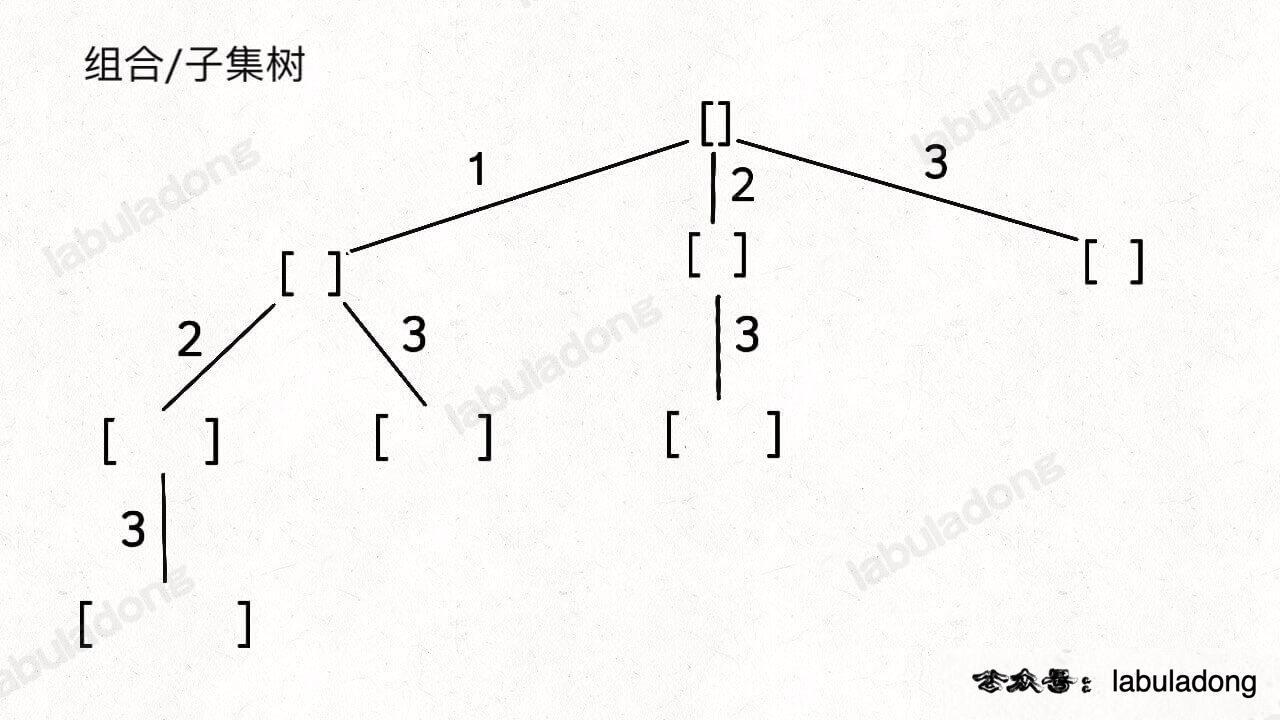
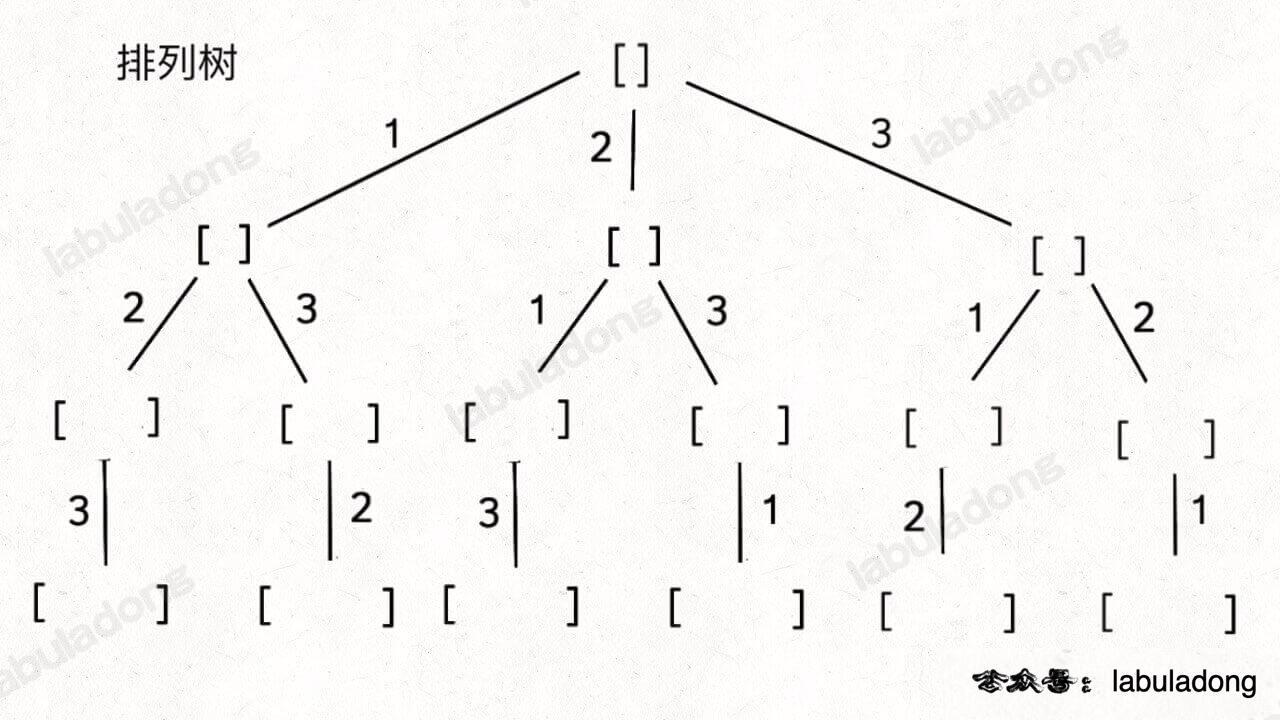
回溯框架
class Solution {
List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
//前置处理,如排序、处理空集等
backtrace(nums, 0);
return ans;
}
void backtrace(int[] nums, int startIndex) {
if(符合条件){
ans.add(new LinkedList<>(track));
return;
}
if(不符合条件)
return;
for (int i = startIndex; i < nums.length; i++) {
cur.add(nums[i]);
backtrace(nums, i + 1);
cur.remove(cur.size() - 1);
}
}
}第一类 - 元素无重,不可复选
子集
无重复元素的数组,不可复选,求所有子集。 Leetcode-78. 子集
套用框架,关键在于用start控制树枝的遍历,避免产生重复的子集
void backtrack(int[] nums, int start) {
// 前序位置,每个节点的值都是一个子集
res.add(new LinkedList<>(track));
for (int i = start; i < nums.length; i++) {
track.addLast(nums[i]);
// 关键:通过 start 控制树枝遍历,避免产生重复子集
backtrack(nums, i + 1);
track.removeLast();
}
}组合
无重复元素的数组,不可复选,求指定元素个数的组合。 Leetcode-77. 组合
所以本质上组合问题和子集问题是一样的,子集不要求元素的个数,组合指定了结果集的大小。
void backtrace(int n, int k, int startIndex) {
// 关键:达到指定个数加入结果集并返回
if(cur.size() == k){
ans.add(new ArrayList<>(cur));
return;
}
for (int i = startIndex; i <= n; i++) {
cur.add(i);
backtrace(n, k, i + 1);
cur.remove(cur.size() - 1);
}
}排列
无重复元素的数组,不可复选,求全排列 Leetcode-46. 全排列
排列问题不同于子集/组合,任何元素顺序不一致都是不同的解,换句话说,任意位置都可以是任意未使用的元素,因此不能再用start控制元素遍历的顺序了。 但是要求元素不可复选,因此关键是要用 used[] 数组判断元素是否已经加入当前的排列结果。
void backtrack(int[] nums) {
// 所有元素都已经加入排列,符合条件,加入结果集并返回
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 关键:已经加入当前排列结果,不可复选
if (used[i])
continue;
track.addLast(nums[i]);
used[i] = true;
backtrack(nums);
used[i] = false;
track.removeLast();
}
}第二类 - 元素可重,不可复选
子集
存在重复元素的数组,不可复选,求所有子集。结果中不能有重复的集合。 Leetcode-90.子集II
回溯树如下,由于相同的元素后续遍历的结果会产生重复,因此需要剪枝: 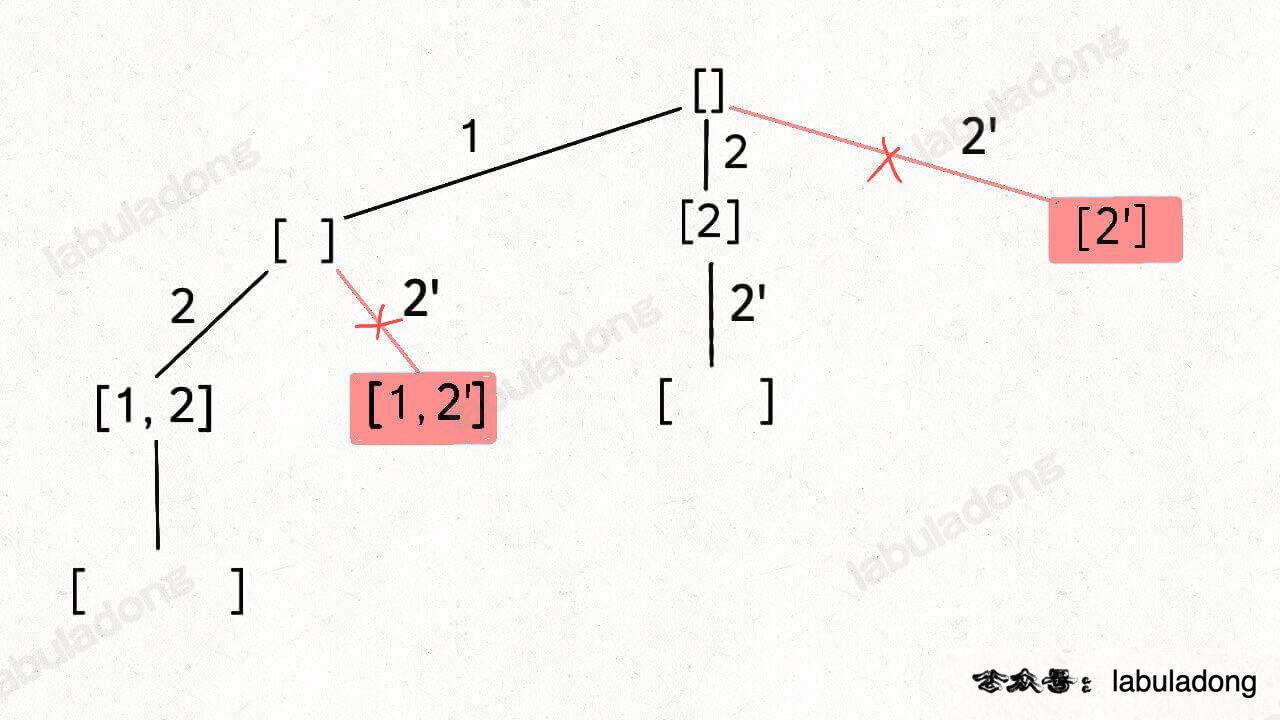
实现上,就先要对数组进行排序让相同的元素挨在一起,方便回溯剪枝
public List<List<Integer>> subsetsWithDup(int[] nums) {
// 前置操作:排序。方便回溯剪枝
Arrays.sort(nums);
backtrack(nums, 0);
return ans;
}
void backtrack(int[] nums, int start) {
ans.add(new LinkedList<>(track));
for (int i = start; i < nums.length; i++) {
//关键:相邻的等值元素产生重复,剪枝
if(i > start && nums[i] == nums[i - 1])
continue;
track.addLast(nums[i]);
backtrack(nums, i + 1);
track.removeLast();
}
}组合
存在重复元素的数组,不可复选,求和为target的组合。结果中不能有重复的集合。 Leetcode-40. 组合总和 II
组合本质上和可重不可复选子集问题是一样的,关键只要记录当前子集的和是否达到target,没达到继续遍历,达到了就加入结果集,超过了就剪枝。
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates, 0, 0, target);
return ans;
}
// sum记录当前track集合总和
void backtrack(int[] nums, int start, int sum, int target) {
// 达到target加入结果集
if (sum == target) {
ans.add(new LinkedList<>(track));
return;
}
// 超过target剪枝
if(sum > target)
return;
for (int i = start; i < nums.length; i++) {
// 和子集一样,相邻的等值树枝会产生重复,剪枝
if (i > start && nums[i] == nums[i - 1])
continue;
track.addLast(nums[i]);
backtrack(nums, i + 1, sum + nums[i], target);
track.removeLast();
}
}排列
存在重复元素的数组,不可复选,求所有不重复的全排列。 Leetcode-47. 全排列 II
解法1:记录前一条树枝的值,对值相同的树枝不遍历,避免产生相同的子树。
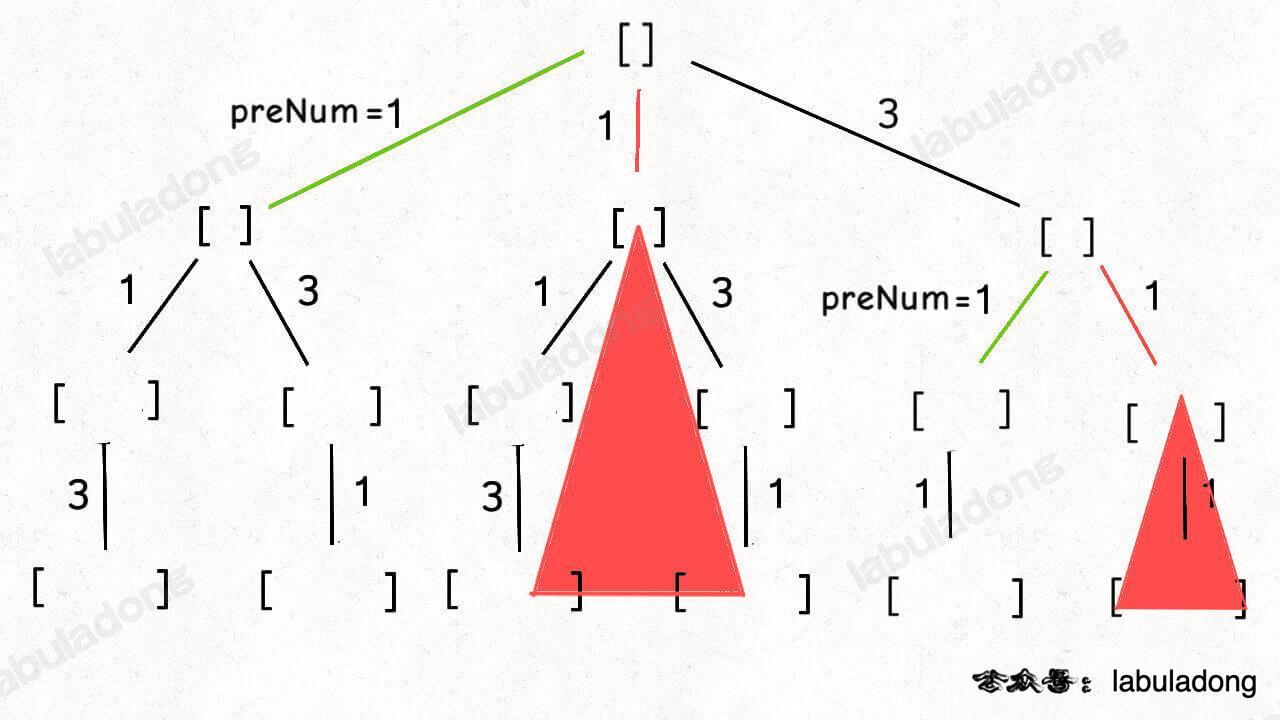
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
used = new boolean[nums.length];
backtrack(nums);
return ans;
}
void backtrack(int[] nums) {
if (track.size() == nums.length) {
ans.add(new LinkedList<>(track));
return;
}
// 解法1关键:记录上一个排列的值,下一个值如果相同则不遍历
int lastNum = -11;
for (int i = 0; i < nums.length; i++) {
if (used[i] || nums[i] == lastNum)
continue;
lastNum = nums[i];
track.addLast(nums[i]);
used[i] = true;
backtrack(nums);
used[i] = false;
track.removeLast();
}
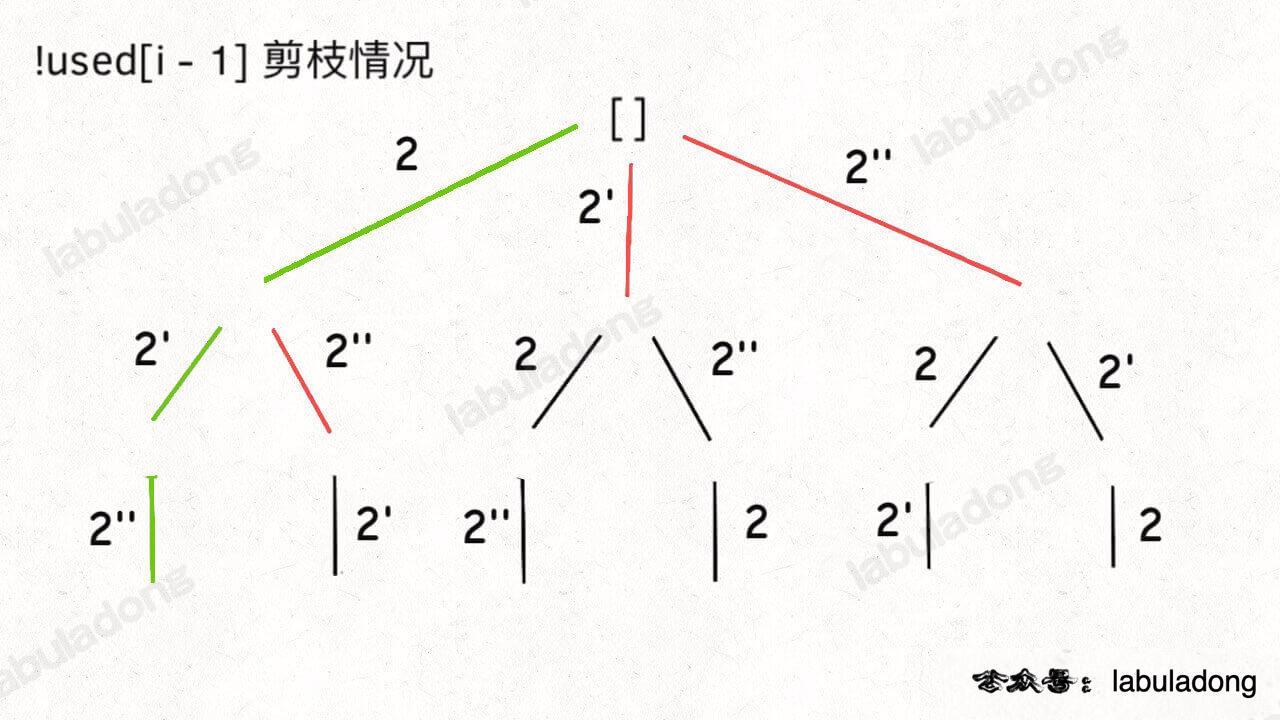
}解法2:控制相同元素的前后顺序。例如 [1,2,2] 看成 [1,2,2'],我们要求2'必须出现在2之后,保证了无重复的排列结果。 (之所以出现重复,是因为把相同元素形成的排列视为了不同的序列,但实际上它们应该是相同的)
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
used = new boolean[nums.length];
backtrack(nums);
return ans;
}
void backtrack(int[] nums) {
// 所有元素都已经加入排列,符合条件,加入结果集并返回
if (track.size() == nums.length) {
ans.add(new LinkedList<>(track));
return;
}
for (int i = 0; i < nums.length; i++) {
if (used[i])
continue;
// 解法2关键:控制相同元素的前后顺序
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])
continue;
track.addLast(nums[i]);
used[i] = true;
backtrack(nums);
used[i] = false;
track.removeLast();
}
}第三类 - 元素无重,可复选
组合
无重复元素的数组,可复选,求和为target的元素组合。 Leetcode-39. 组合总和
标准的子集/组合问题我们使用start + 1使得下一层递归时不可复选元素,现在可以复选了,那么去掉+1就可以了。无重可复选的子集问题也类似。
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates, 0, 0, target);
return ans;
}
void backtrack(int[] nums, int start, int sum, int target){
if(sum == target)
ans.add(new LinkedList<>(track));
if(sum >= target)
return;
for (int i = start; i < nums.length; i++) {
track.addLast(nums[i]);
// 关键:下一层递归仍从i开始遍历,也即可复选元素
backtrack(nums, i, sum + nums[i], target);
track.removeLast();
}
}排列
LeetCode没有这样的例题,但其实思路和上面的组合一样,现在元素可复选就更简单了,直接去掉used数组就可以了。
void backtrack(int[] nums) {
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
track.add(nums[i]);
backtrack(nums);
track.removeLast();
}
}总结
- 子集和组合本质上一样,区别在于组合指定了集合大小
- 无重不可复选通过start + 1控制元素不复选
- 有重不可复选通过判断 nums[i] == nums[i - 1] 来避免相同元素产生重复集合
- 无重可复选只要去除 start 的 +1 操作,让元素可复选即可
- 排列的重点在于任意位置放不同元素产生的序列是不一样的,因此需要 used[] 数组判断当前元素是否已经加入排列
- 有重不可复选有两种特殊解法,一种是记录上一次加入排列的元素,另一种是控制相同元素在排列中的顺序
- 无重可复选只要去除used数组,让元素可复选即可
- 元素可重问题通常都要先对数组排序,方便后续的回溯剪枝