LeetCode 136. 只出现一次的数字

链接：https://leetcode.cn/problems/single-number/

LeetCode136

找出数组中唯一成单的数字，主要学习异或运算的性质和哈希表的使用。

解法1. 异或运算

异或运算的三个性质

• 任何数和0做异或，结果仍是原来的数 $$ a \bigoplus 0 = a $$

• 任何数和自身做异或结果是0 $$ a \bigoplus a = 0 $$

• 异或运算满足交换律和结合律 $$ a \bigoplus b \bigoplus a = b \bigoplus a \bigoplus a = b $$

因此数组中所有元素异或即可得到单个的元素。时间复杂度$O(n)$

class Solution {
    public int singleNumber(int[] nums) {
        int ans = nums[0];
        for(int i = 1; i < nums.length; i++){
            ans ^= nums[i];
        }

        return ans;
    }
}

解法2. 哈希表

使用哈希表存储每个数字和该数字出现的次数。最后次数为1的就是单个数字

Class Solution {
    public int singleNumber(int[] nums) {
        Map<Integer, Integer> map = new HashMap<>();
        for(Integer i : nums){
            Integer count = map.get(i);
            map.put(i, count == null ? 1 : ++count;);
        }

        for(Integer i : nums){
            if(map.get(i) == 1)
                return i;
        }
}

时间复杂度$O(n)$,空间复杂度$O(n)$

---

LeetCode 191. 位1的个数 (汉明重量)

链接：https://leetcode.cn/problems/number-of-1-bits/

LeetCode191

方法1 - 移位

循环检查二进制的每一位是否为1，例如让n和 $2^i$ 进行与运算，或者让n和1相与并右移n，得到二进制末尾是否为1 时间复杂度$O(k)$, 其中$k$是二进制位数

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        while (n != 0) {
            count += n & 1;
            n >>>= 1;
        }
        return count;
    }
}

注，Java中：

• << 左移，高位舍弃，低位补0
• >> 右移，舍弃最低位，高位用符号位填补，正数补0，负数补1
• >>> 无符号右移，舍弃最低位，高位用0填补

方法二 - Brian Kernighan 算法

利用 $n \And (n-1)$ 能够把二进制中的最低位1变为0的特性，反复操作，直至n=0

n&n-1

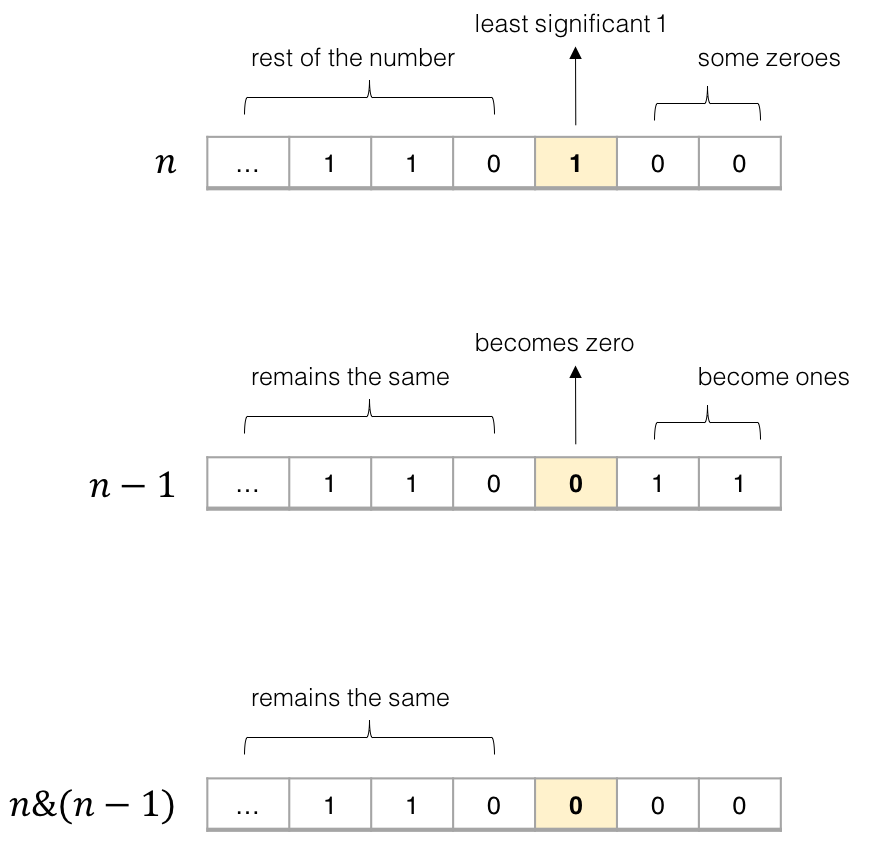
可以看到，n-1会把n末尾的0变1，直到遇到最低位的1把它变0，其余保持不变。相与时，n末尾的0与运算后仍是0，而最低位1和0相与得0，其余位不变。因此，$n \And (n-1)$把n的最低位1变成了0，其余位不变。

时间复杂度$O(logn)$, 循环次数就是n的二进制中1的个数

public class Solution {
    public int hammingWeight(int n) {
        int ret = 0;
        while (n != 0) {
            n &= n - 1;
            ret++;
        }
        return ret;
    }
}

方法3 - 分治 (Variable-Precision SWAR 算法)

0x55555555 = 0B0101...0101 0x33333333 = 0B0011...0011 0x0f0f0f0f = 0B00001111...00001111

贴上Java中的Integer::bitCount()源码，太神奇了！

public static int bitCount(int i) {
        i = i - ((i >>> 1) & 0x55555555);                   // 此时i每两位的值是原数字每两位1的个数
        i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);    // 此时i每4位的值是原数字每4位1的个数 
        i = (i + (i >>> 4)) & 0x0f0f0f0f;                   // 此时i每8位的值是原数字每8位1的个数
        i = i + (i >>> 8);                                  // 每两个8位合并统计
        i = i + (i >>> 16);                                 // 两个16位合并统计
        return i & 0x3f;                                    // 取出低6位，因为32bit最高只有32个1
    }

注意第二行，前半句保留奇数组的"两位"，后半句保留偶数组的"两位"，然后相加使得相邻的两个"两位"合并统计，即得到每4位1的个数 分开&的原因在于2bit最多表示3个1，不足以表示原数字每4位1的个数，因此要多做一次&然后相加 而在第三行，4bit(0-15)可以表示8位二进制1的个数，因此只需要&一次

---

LeetCode 461. 汉明距离

链接：https://leetcode.cn/problems/hamming-distance/

LeetCode461

先把两数字异或，然后同LeetCode191，统计1的个数。

class Solution {
    public int hammingDistance(int x, int y) {
        int s = x ^ y, ret = 0;
        while (s != 0) {
            s &= s - 1;
            ret++;
        }
        return ret;
    }
}